Philipp Herholz

2023

Designing Personalized Garments with Body Movement Eurographics 2023 (CGF)

Katja Wolff, Philipp Herholz, Verena Ziegler, Frauke Link, Nico Brügel, Olga Sorkine-Hornung
Project page PDF Video BibTeX

The standardized sizes used in the garment industry do not cover the range of individual differences in body shape for most people, leading to ill-fitting clothes, high return rates and overproduction. Recent research efforts in both industry and academia therefore focus on virtual try-on and on-demand fabrication of individually fitting garments. We propose an interactive design tool for creating custom-fit garments based on 3D body scans of the intended wearer. Our method explicitly incorporates transitions between various body poses to ensure a better fit and freedom of movement. The core of our method focuses on tools to create a 3D garment shape directly on an avatar without an underlying sewing pattern, and on the adjustment of that garment’s rest shape while interpolating and moving through the different input poses. We alternate between cloth simulation and rest shape adjustment based on stretch to achieve the final shape of the garment. At any step in the real-time process, we allow for interactive changes to the garment. Once the garment shape is finalized for production, established techniques can be used to parameterize it into a 2D sewing pattern or transform it into a knitting pattern.

2022

Sparsity-Specific Code Optimization using Expression Trees SIGGRAPH 2022 (TOG)

Philipp Herholz, Xuan Tang, Teseo Schneider, Shoaib Kamil, Daniele Panozzo, Olga Sorkine-Hornung
Project page PDF Code BibTeX

We introduce a code generator that converts unoptimized C++ code operating on sparse data into vectorized and parallel CPU or GPU kernels. Our approach unrolls the computation into a massive expression graph, performs redundant expression elimination, grouping, and then generates an architecture-specific kernel to solve the same problem, assuming that the sparsity pattern is fixed, which is a common scenario in many applications in computer graphics and scientific computing. We show that our approach scales to large problems and can achieve speedups of two orders of magnitude on CPUs and three orders of magnitude on GPUs, compared to a set of manually optimized CPU baselines. To demonstrate the practical applicability of our approach, we employ it to optimize popular algorithms with applications to physical simulation and interactive mesh deformation.

Variational Quadratic Shape Functions for Polygons and Polyhedra SIGGRAPH 2022

Astrid Bunge, Philipp Herholz, Olga Sorkine-Hornung, Mario Botsch, Misha Kazhdan
Project page PDF Code BibTeX

Solving partial differential equations (PDEs) on geometric domains is an important component of computer graphics, geometry processing, and many other fields. Typically, the given discrete mesh is the geometric representation and should not be altered for simulation purposes. Hence, accurately solving PDEs on general meshes is a central goal and has been considered for various differential operators over the last years. While it is known that using higher-order basis functions on simplicial meshes can substantially improve accuracy and convergence, extending these benefits to general surface or volume tessellations in an efficient fashion remains an open problem. Our work proposes variationally optimized piecewise quadratic shape functions for polygons and polyhedra, which generalize quadratic P2 elements, exactly reproduce them on simplices, and inherit their beneficial numerical properties. To mitigate the associated cost of increased computation time, particularly for volumetric meshes, we introduce a custom two-level multigrid solver which significantly improves computational performance.

2021

Developable Approximation via Gauss Image Thinning SGP 2021

Alexandre Binninger, Floor Verhoeven, Philipp Herholz, Olga Sorkine-Hornung
Project page PDF Video BibTeX

Approximating 3D shapes with piecewise developable surfaces is an active research topic, driven by the benefits of developable geometry in fabrication. Piecewise developable surfaces are characterized by having a Gauss image that is a 1D object -- a collection of curves on the Gauss sphere. We present a method for developable approximation that makes use of this classic definition from differential geometry. Our algorithm is an iterative process that alternates between thinning the Gauss image of the surface and deforming the surface itself to make its normals comply with the Gauss image. The simple, local-global structure of our algorithm makes it easy to implement and optimize. We validate our method on developable shapes with added noise and demonstrate its effectiveness on a variety of non-developable inputs. Compared to the state of the art, our method is more general, tessellation independent, and preserves the input mesh connectivity.

2020

Sparse Cholesky Updates for Interactive Mesh Parameterization Siggraph Asia 2020

Philipp Herholz, Olga Sorkine-Hornung
Project page PDF Video BibTeX

We present a novel linear solver for interactive parameterization tasks. Our method is based on the observation that quasi-conformal parameterizations of a triangle mesh are largely determined by boundary conditions. These boundary conditions are typically constructed interactively by users, who have to take several artistic and geometric constraints into account while introducing cuts on the geometry. Commonly, the main computational burden in these methods is solving a linear system every time new boundary conditions are imposed. The core of our solver is a novel approach to efficiently update the Cholesky factorization of the linear system to reflect new boundary conditions, thereby enabling a seamless and interactive workflow even for large meshes consisting of several millions of vertices.

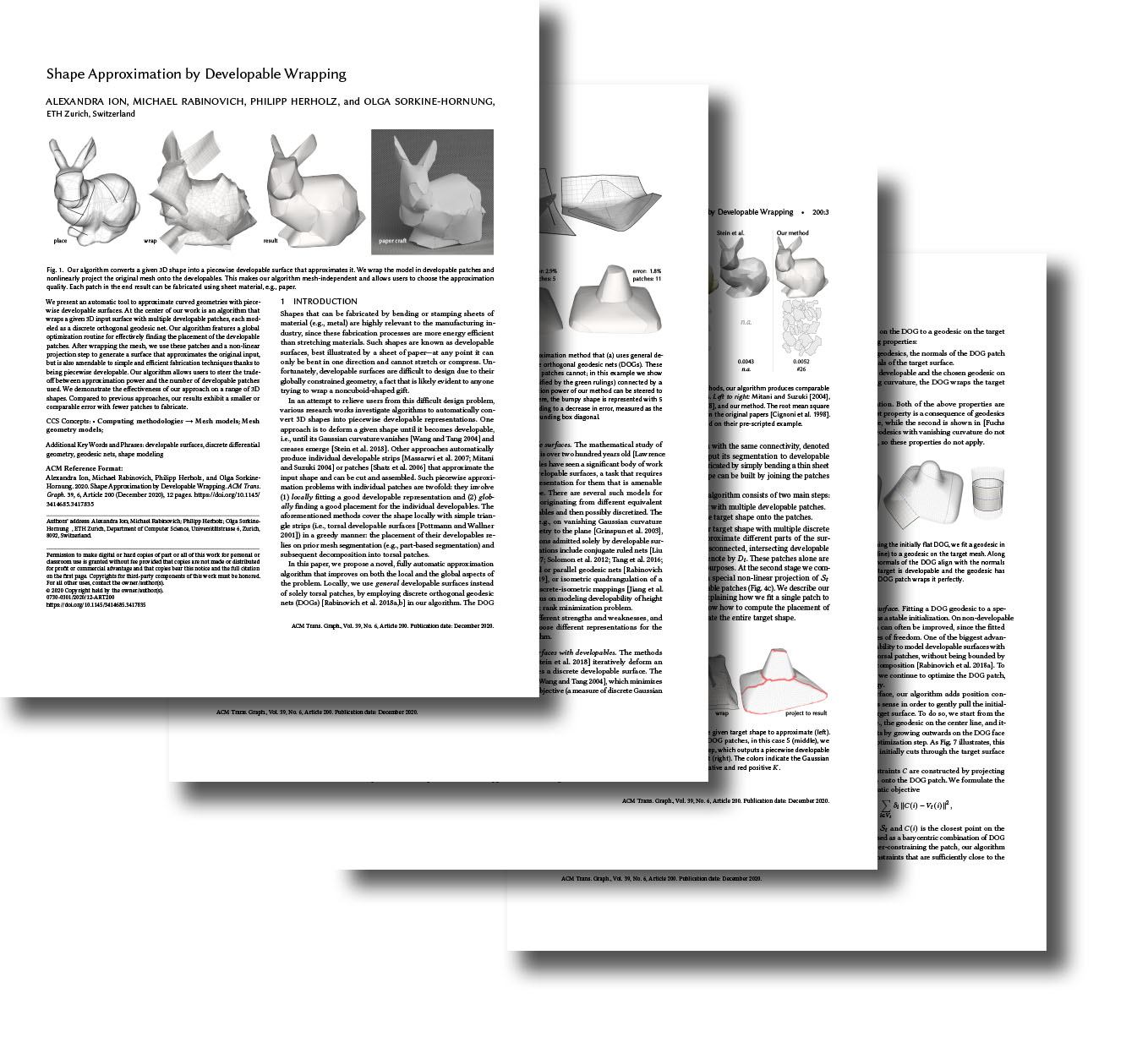
Shape Approximation by Developable Wrapping Siggraph Asia 2020

Alexandra Ion, Michael Rabinovich, Philipp Herholz, Olga Sorkine-Hornung
Project page PDF Video BibTeX

We present an automatic tool to approximate curved geometries with piecewise developable surfaces. At the center of our work is an algorithm that wraps a given 3D input surface with multiple developable patches, each modeled as a discrete orthogonal geodesic net. Our algorithm features a global optimization routine for effectively finding the placement of the developable patches. After wrapping the mesh, we use these patches and a non-linear projection step to generate a surface that approximates the original input, but is also amendable to simple and efficient fabrication techniques thanks to being piecewise developable. Our algorithm allows users to steer the tradeoff between approximation power and the number of developable patches used. We demonstrate the effectiveness of our approach on a range of 3D shapes. Compared to previous approaches, our results exhibit a smaller or comparable error with fewer patches to fabricate.

Properties of Laplace Operators for Tetrahedral Meshes SGP 2020

Marc Alexa, Philipp Herholz, Maximilian Kohlbrenner Olga Sorkine-Hornung
Project page PDF Slides Talk Code BibTeX

Discrete Laplacians for triangle meshes are a fundamental tool in geometry processing. The so-called cotan Laplacian is widely used since it preserves several important properties of its smooth counterpart. It can be derived from different principles: either considering the piecewise linear nature of the primal elements or associating values to the dual vertices. Both approaches lead to the same operator in the two-dimensional setting. In contrast, for tetrahedral meshes, only the primal construction is reminiscent of the cotan weights, involving dihedral angles. We provide explicit formulas for the lesser-known dual construction. In both cases, the weights can be computed by adding the contributions of individual tetrahedra to an edge. The resulting two different discrete Laplacians for tetrahedral meshes only retain some of the properties of their two-dimensional counterpart. In particular, while both constructions have linear precision, only the primal construction is positive semi-definite and only the dual construction generates positive weights and provides a maximum principle for Delaunay meshes. We perform a range of numerical experiments that highlight the benefits and limitations of the two constructions for different problems and meshes.

Polygon Laplacian Made Simple Eurographics 2020

Astrid Bunge, Philipp Herholz, Misha Kazhdan, Mario Botsch
PDF BibTeX

The discrete Laplace-Beltrami operator for surface meshes is a fundamental building block for many (if not most) geometry processing algorithms. While Laplacians on triangle meshes have been researched intensively, yielding the cotangent discretization as the de-facto standard, the case of general polygon meshes has received much less attention. We present a discretization of the Laplace operator which is consistent with its expression as the composition of divergence and gradient operators, and is applicable to general polygon meshes, including meshes with non-convex, and even non-planar, faces. By virtually inserting a carefully placed point we implicitly refine each polygon into a triangle fan, but then hide the refinement within the matrix assembly. The resulting operator generalizes the cotangent Laplacian, inherits its advantages, and is empirically shown to be on par or even better than the recent polygon Laplacian of Alexa and Wardetzky --- while being simpler to compute.

2019

Reflection Symmetry in Textured Sewing Patterns VMV 2019

Katja Wolff, Philipp Herholz, Olga Sorkine-Hornung
Project page PDF BibTeX

Recent work in the area of digital fabrication of clothes focuses on repetitive print patterns, specifically the 17 wallpaper groups, and their alignment along garment seams. While adjusting the underlying sewing patterns for maximized fit of wallpapers along seams, past research does not account for global symmetries that underlie almost every sewing pattern due to the symmetry of the human body. We propose an interactive tool to define such symmetries and integrate them into the existing algorithm, such that both the texture alignment and the deformation of the sewing pattern adhere to these symmetries.

Efficient Computation of Smoothed Exponential Maps Eurographics 2019 (CGF paper)

Philipp Herholz, Marc Alexa
PDF Slides BibTeX DOI

Many applications in geometry processing require the computation of local parameterizations on a surface mesh at interactive rates. A popular approach is to compute local exponential maps, i.e. parameterizations that preserve distance and angle to the origin of the map. We extend the computation of geodesic distance by heat diffusion to also determine angular information for the geodesic curves. This approach has two important benefits compared to fast approximate as well as exact forward tracing of the distance function: First, it allows generating smoother maps, avoiding discontinuities. Second, exploiting the factorization of the global Laplace–Beltrami operator of the mesh and using recent localized solution techniques, the computation is more efficient even compared to fast approximate solutions based on Dijkstra's algorithm.

Understanding Metamaterial Mechanisms CHI 2019

Alexandra Ion, David Lindlbauer, Philipp Herholz, Marc Alexa, Patrick Baudisch
PDF Slides BibTeX

In this paper, we establish the underlying foundations of mechanisms that are composed of cell structures - known as metamaterial mechanisms. Such metamaterial mechanisms were previously shown to implement complete mechanisms in the cell structure of a 3D printed material, without the need for assembly. However, their design is highly challenging. A mechanism consists of many cells that are interconnected and impose constraints on each other. This leads to unobvious and non-linear behavior of the mechanism, which impedes user design. In this work, we investigate the underlying topological constraints of such cell structures and their influence on the resulting mechanism. Based on these findings, we contribute a computational design tool that automatically creates a metamaterial mechanism from user-defined motion paths. This tool is only feasible because our novel abstract representation of the global constraints highly reduces the search space of possible cell arrangements.

2018

Factor Once: Reusing Cholesky Factorizations on Sub-Meshes SIGGRAPH ASIA 2018

Philipp Herholz, Marc Alexa
Project page PDF Slides BibTeX DOI

A common operation in geometry processing is solving symmetric and positive semi-definite systems on a subset of a mesh with conditions for the vertices at the boundary of the region. This is commonly done by setting up the linear system for the sub-mesh, factorizing the system (potentially applying preordering to improve sparseness of the factors), and then solving by back-substitution. This approach suffers from a comparably high setup cost for each local operation. We propose to reuse factorizations defined on the full mesh to solve linear problems on sub-meshes. We show how an update on sparse matrices can be performed in a particularly efficient way to obtain the factorization of the operator on a sun-mesh significantly outperforming general factor updates and complete refactorization. We analyze the resulting speedup for a variety of situations and demonstrate that our method outperforms factorization of a new matrix by a factor of up to 10 while never being slower in our experiments.

OptiSpace: Automated Placement of Interactive 3D Projection Mapping Content Conference on Human Factors in Computing Systems (CHI) 2018

Andreas Fender, Philipp Herholz, Marc Alexa and Joerg Mueller
Movie BibTeX DOI

We present OptiSpace, a system for the automated placement of perspectively corrected projection mapping content. We analyze the geometry of physical surfaces and the viewing behavior of users over time using depth cameras. Our system measures user view behavior and simulates a virtual projection mapping scene users would see if content were placed in a particular way. OptiSpace evaluates the simulated scene according to perceptual criteria, including visibility and visual quality of virtual content. Finally, based on these evaluations, it optimizes content placement, using a two-phase procedure involving adaptive sampling and the covariance matrix adaptation algorithm. With our proposed architecture, projection mapping applications are developed without any knowledge of the physical layouts of the target environments. Applications can be deployed in different uncontrolled environments, such as living rooms and office spaces.

2017

Localized solutions of sparse linear systems for geometry processing SIGGRAPH ASIA 2017

Philipp Herholz, Timothy A. Davis and Marc Alexa
Project page PDF Slides BibTeX DOI

Computing solutions to linear systems is a fundamental building block of many geometry processing algorithms. In many cases the Cholesky factorization of the system matrix is computed to subsequently solve the system, possibly for many right-hand sides, using forward and back substitution. We demonstrate how to exploit sparsity in both the right-hand side and the set of desired solution values to obtain significant speedups. The method is easy to implement and potentially useful in any scenarios where linear problems have to be solved locally. We show that this technique is useful for geometry processing operations, in particular we consider the solution of diffusion problems. All problems profit significantly from sparse computations in terms of runtime, which we demonstrate by providing timings for a set of numerical experiments.

HeatSpace: Automatic Placement of Displays by Empirical Analysis of User Behavior ACM Symposium on User Interface Software and Technology (UIST) 2017

Andreas Fender, David Lindlbauer, Philipp Herholz, Marc Alexa and Joerg Mueller
Movie BibTeX DOI

We present HeatSpace, a system that records and empirically analyzes user behavior in a space and automatically suggests positions and sizes for new displays. The system uses depth cameras to capture 3D geometry and users’ perspectives over time. To derive possible display placements, it calculates volumetric heatmaps describing geometric persistence and planarity of structures inside the space. It evaluates visibility of display poses by calculating a volumetric heatmap describing occlusions, position within users’ field of view, and viewing angle. Optimal display size is calculated through a heatmap of average viewing distance. Based on the heatmaps and user constraints we sample the space of valid display placements and jointly optimize their positions. This can be useful when installing displays in multi-display environments such as meeting rooms, offices, and train stations.

Unsharp Masking Geometry Improves 3D Prints Shape Modeling International (SMI) 2017

Philipp Herholz, Sebastian Koch, Tamy Boubekeur and Marc Alexa
Project page PDF BibTeX DOI

Mass market digital manufacturing devices are severely limited in accuracy and material, resulting in a significant gap between the appearance of the virtual and the real shape. In imaging as well as rendering of shapes, it is common to enhance features so that they are more apparent. We provide an approach for feature enhancement that directly operates on the geometry of a given shape, with particular focus on improving the visual appearance for 3D printing. The technique is based on unsharp masking, modified to handle arbitrary free-form geometry in a stable, efficient way, without causing large scale deformation. On a series of manufactured shapes we show how features are lost as size of the object decreases, and how our technique can compensate for this. We evaluate this effect in a human subject experiment and find significant preference for modified geometry.

Diffusion Diagrams: Voronoi Cells and Centroids from Diffusion EUROGRAPHICS 2017

Philipp Herholz, Felix Haase and Marc Alexa
Project page PDF BibTeX Movie Slides DOI

We define Voronoi cells and centroids based on heat diffusion. These heat cells and heat centroids coincide with the common definitions in Euclidean spaces. On curved surfaces they compare favorably with definitions based on geodesics: they are smooth and can be computed in a stable way with a single linear solve. We analyze the numerics of this approach and can show that diffusion diagrams converge quadratically against the smooth case under mesh refinement, which is better than other common discretization of distance measures in curved spaces. By factorizing the system matrix in a preprocess, computing Voronoi diagrams or centroids amounts to just back-substitution. We show how to localize this operation so that the complexity is linear in the size of the cells and not the underlying mesh. We provide several example applications that show how to benefit from this approach.

2015

Approximating Free-form Geometry with Height Fields for Manufacturing EUROGRAPHICS 2015

Philipp Herholz, Wojciech Matusik and Marc Alexa
Project page PDF Slides Movie BibTeX DOI

We consider the problem of manufacturing free-form geometry with classical manufacturing techniques, such as mold casting or 3-axis milling. We determine a set of constraints that are necessary for manufacturability and then decompose and, if necessary, deform the shape to satisfy the constraints per segment. We show that many objects can be generated from a small number of (mold-)pieces if some deformation is acceptable. We provide examples of actual molds and the resulting manufactured objects.

Perfect Laplacians for Polygon Meshes Eurographics Symposium on Geometry Processing (SGP) 2015

Philipp Herholz, Jan Eric Kyprianidis and Marc Alexa
Project page PDF Slides BibTeX DOI

A discrete Laplace-Beltrami operator is called perfect if it possesses all the important properties of its smooth counterpart. It is known which triangle meshes admit perfect Laplace operators and how to fix any other mesh by changing the combinatorics. We extend the characterization of meshes that admit perfect Laplacians to general polygon meshes. More importantly, we provide an algorithm that computes a perfect Laplace operator for any polygon mesh without changing the combinatorics, although, possibly changing the embedding. We evaluate this algorithm and demonstrate it at applications.